Let's say we've got a Markov Decision Process, and a policy π. How good is this policy?
Well, one way to figure it out is by simply iterating the policy over a value function for each state.
In this example, we have a small gridworld. The goal is to make it to one of the two gray corners, ending the game. To encourage this, every move will have a reward of -1. Our policy will simply be to move in a random direction.
In order to find the value of the policy, we can start from a value function of all 0 and iterate, adding the reward for each state after every iteration.
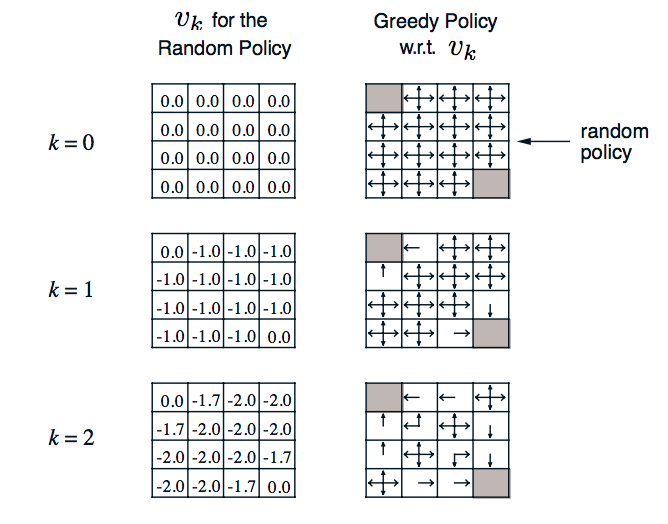
In each step, the value of a state is the sum of the previous values of all neighbors, plus the reward of -1, scaled by probability (0.25 for up,down,right,left). Since the gray corners mark the end of the game, the reward is just 0.
After only two iterations, it already becomes clear that being near the two gray corners will have a higher return than being near the center.
But that only shows how to evaluate a certain policy. Randomly choosing a direction is certainly not the best strategy.
In policy iteration, instead of sticking to the same policy every time the values are iterated, the policy acts greedily towards the best expected result. In the example above, following the direction of the arrows would be the greedy policy.
Eventually, the policy would reach a point where continuing to iterate would no longer change anything. That final policy would therefore be the optimal policy for that environment.
The loop for policy iteration is as follows:
- perform policy evaluation for some number of iterations
- change the policy to act greedy towards the new value function
- repeat
On the other hand, value iteration only cares about the value function, and not on forming a complete policy for every iteration. It's the same as policy iteration, but only performing policy evaluation once and then changing the policy right away.
While this requires less steps to find the optimal policy, intermediate steps cannot be used as a suboptimal policy as the values do not correspond to a concrete policy.
Note: this is a continuation from a previous post, with information taken from David Silver's RL Course.