How many shapes can be made from six 2x4 LEGO bricks? The answer is 915,103,765. By combining only a few simple parts, it’s surprisingly easy to achieve high levels of complexity.

A Lego Counting Problem: http://web.math.ku.dk/~eilers/lego.html

If you look at the single-celled organisms on Earth today, you’ll mostly be stuck with bacteria. But once you enter the multi-cellular domain, suddenly life shows all sorts of shapes and structures. The possibilty space of multi-celled organisms is much richer.

Recall our principles of open-endedness:

  • Possibility Space: A world consists of a set of organisms. The space of possible organisms must be arbitrarily large.
  • Peer Dependency: When new organisms appear, an environment must develop new niches.
  • Search Algorithm: A procedure must find new organisms to fit new niches.

In this post, let’s dive into how multi-cellularity can expand our possibility space towards increasingly complex genomes.

Multicell World

Last time, we worked with a simple Cellworld where cells could gain energy and reproduce. Starting with this is a base, let’s restructure the genome to support multi-cellularity, and also mix in the our bitwise chemical system.

In the Multicell world, an organism is made of a group of cells. Each cell performs a single chemical reaction, creating energy. When a cell has gathered enough energy, it will create a new cell in a neighboring space.

Similar to the Bitwise Chemicals project, there are eight chemicals. Every space in the grid has its own chemical counts, and a cell will only be able to perform a reaction if the required chemicals are there. Within an organism’s cells, chemical counts and energy are averaged out.

Green cells represent the reaction (01+02). These chemicals are provided periodically, at a higher rate near the bottom.
A brown reaction appears, which reacts the waste produced by the green reaction.
A wide variety of cells coexist, living off the outputs of neighboring reactions.

So, we now have a world that supports multi-cell organisms, and they can interact with each other and evolve. But there’s an obvious flaw: every cell is doing the same thing!

While we have different species performing different reactions, within an organism all the cells are the same. Let’s allow for cells to specialize, and perform different roles.

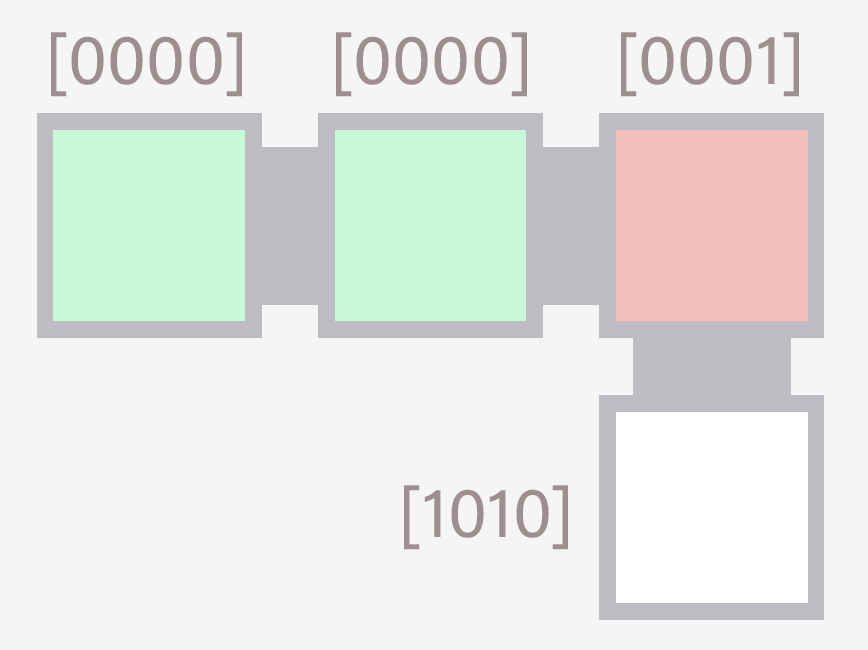
An organism comprised of different specialized cells. Cells behave differently depending on their pheromone.
In this setup, a genome is a decision tree. When a new cell is born, this tree will tell it what reaction to specialize in. Once a cell specializes, it will only perform that reaction.

Crucially, the genome decision tree takes as input a pheromone – four bits that are unique to each indicidual cell. When a cell makes a child, it can assign it a new pheromone, which can cause the child to specialize in a different reaction.

Put together, the genome of a organism is like an algorithm that tells the organism how to grow and what its cells should specialize in. Will species evolve to take advantage of multi-cellularity?
In the beginning, cells consist only of green reactions, living mostly near the bottom.
A species with both green and brown cells is twice as energy-efficient, since the output of green is used to power the brown reaction.
The next generation begins to differentiate, and we see diverse combinations of multi-cell reactions.
Here, the first species develops Killer cells. Killer cells cost energy, and have to be powered by neighboring reaction cells.
Descendants of the first Killer species spread. They develop different base reactions to power themselves.
The world eventually settles into species containing a few reaction cells along with sporadic Killer cells.

Through the multi-cell experiment, we see a bunch of species appear that use multiple specialized cells to perform chains of reactions. These reactions usually synergize, with one providing the materials for the other. As the world advances, we also see cells that use their excess energy to power Killer cells and gain space.

One interesting note are the patterns of cells. With the way genomes work, there’s no real definition of a “pattern” – it all depends on the dynamics of the pheromones. Perhaps a cell with a pheromone of [0001] will produce a child of pheromone [0010], whose own child will loop back to [0001].

In real-life plants, we often see the Fibonacci series, or spiral patterns. These are patterns that naturally arise when cells grow by replication, since they are easy ways to gain repetition. In our gridworld, we often see checker-board style patterns, which are similarly easy to achieve.

Further work can involve:

  • How can we increase the complexity of inter-species interactions beyong sharing chemicals and/or killing each other? What kinds of complexity lead to novel/interesing behavior?
  • Other than grid-based worlds, are there more interesting ways to represent physical organisms? What is the simplest physics system that will allow for movement?

Appendix


Here is a full run of the Multicell world. Shown on the left are average chemical counts throughout the grid, and on the right is a legend for what reactions each color represents.