Insight: IQL-AWR agents on 'maze2d' converge to a standard deviation of 0.4, which is much higher than expected.
Hypothesis: The KL constraint of AWR prevents it from learning Gaussian policies that are centered around the optimal action.
Conclusion: In data-heavy settings, use DDPG or discretized AWR for policy extraction. For sparse data, use AWR because DDPG will overfit.

When doing offline RL with IQL, we learn an implicit Q-function without learning a policy. The policy must be extracted later using the information from Q(s,a). In the original IQL paper, advantage-weighted regression (AWR) is used for policy extraction. The AWR objective is a weighted behavior cloning loss with the form:

max  log  π(a∣s)∗exp(λ∗A(s,a))max \; log \; \pi(a|s) * exp(\lambda * A(s,a))

The AWR objective can be derived as the solution to constrained optimization problem of

  1. Maximize E[π(a∣s)∗A(s,a)]E[ \pi(a|s) * A(s,a) ]
  2. st. KL(πdata∣π)<ϵKL(\pi_{data} | \pi) < \epsilon

The λ\lambda term is a temperature parameter that controls how tight the constraint is.

A nice property of AWR is that it avoids querying out-of-data actions. We only weight state-action pairs inside the dataset, instead of searching over the $A(s,a)$ space which may have inaccurate values.

But a downside of AWR is that we assign probability mass to each action in the dataset. Since we usually use a Gaussian policy, this leads to bad behavior.

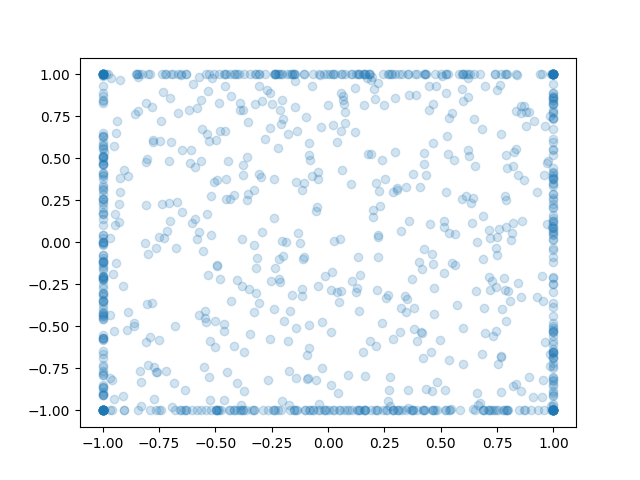
As an example, let's look at maze-2d. Here the actions are (x,y) velocities to move an agent to a goal. It's not complicated; and intuitively the best actions should be along the edge of the unit sphere. But, the policy doesn't behave that way.

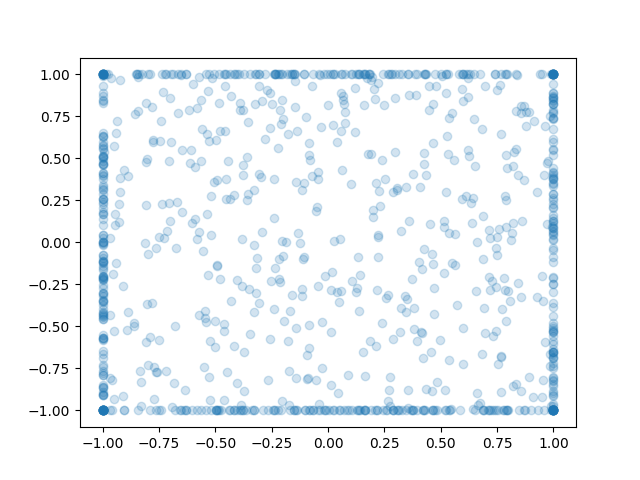
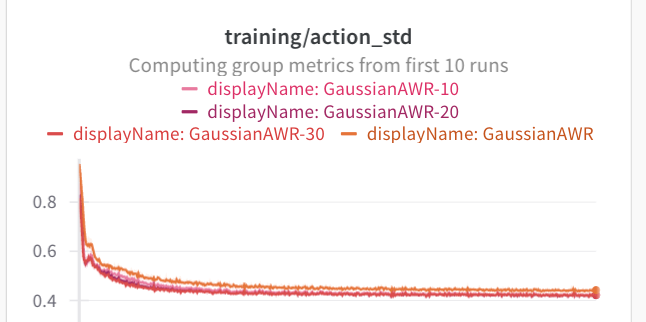
Left: Data actions. Right: Actions produced by IQL-AWR policy.

If we look at the standard deviations of the Gaussian heads, they are not at zero. They are at 0.4, which is quite a bit of variance.

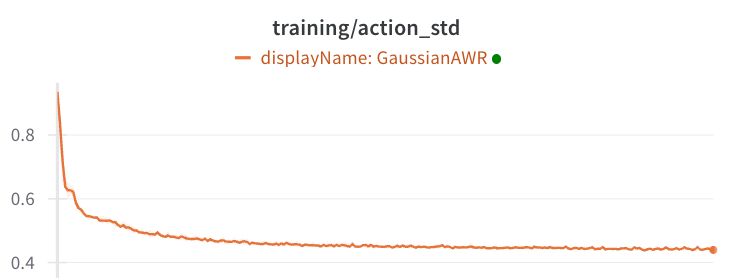
Remember that Gaussian heads have a log-probability that is equivalent to L2 loss scaled by variance. They suffer from the issue of mean-matching rather than mode-matching. With AWR, we find a 'compromise' between behavior cloning and advantage-maximization, and this compromise might not make sense.

Gaussians cannot capture multi-modal distributions. The most likely point is not the mode, but the mean.

Let's try some fixed. What if we extract the policy via DDPG? DDPG-style extraction optimizes through the Q-function to find the best action at each state. Importantly, DDPG ignores the shape of the Q-function landscape, and only cares about where the maximum is.

Another path is to discretize the action space. If we bin the action space into tokens, we can handle multimodality easily. So we don't run into the mean-matching problem. The token with highest advantage will also have the highest probability.

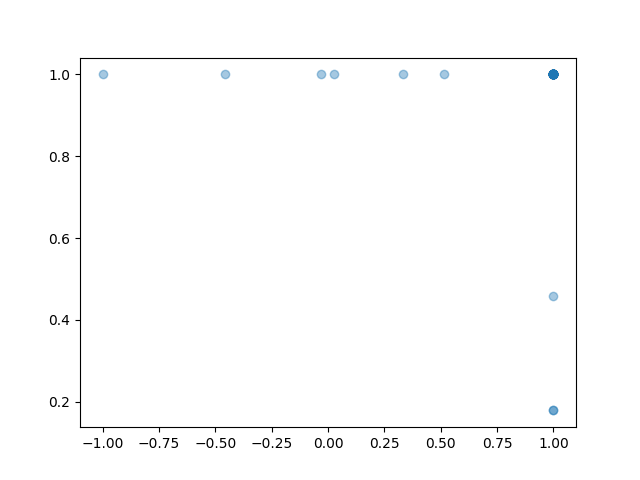
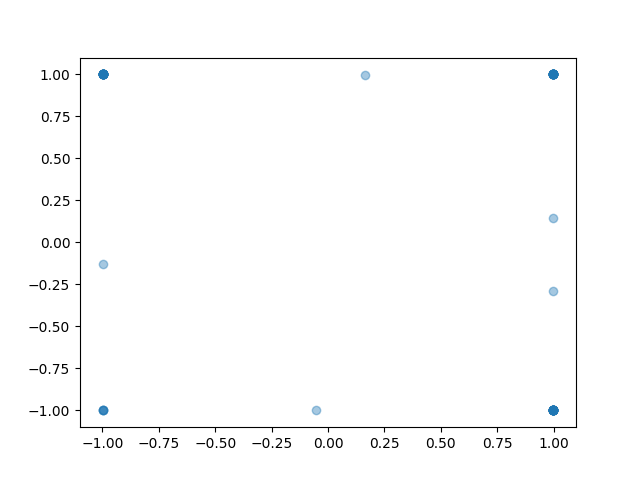
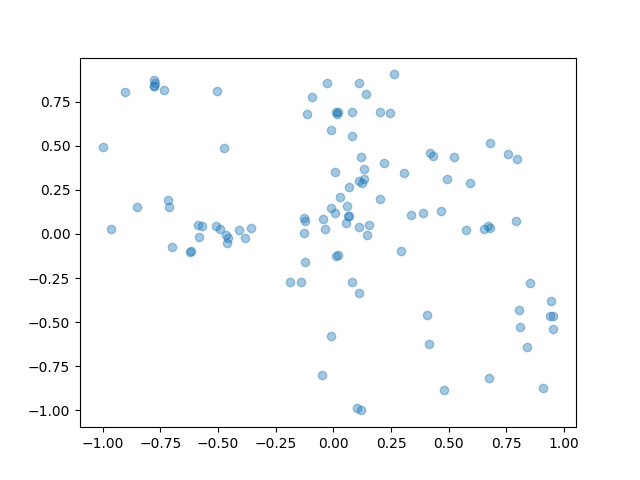
Left: Data actions. Middle: DDPG actions. Right: AWR-Discrete actions.

That looks much more reasonable. The actions are all on the unit circle now, which is consistent with the data. DDPG picks only the highest-advantage actions, whereas the AWR policy still assigns some probability mass to all data actions, but does so in a multimodal way that preserves the correct locations.

Question: What about the temperature parameter? As lambda goes to infinity, then the KL constraint becomes zero and AWR approaches the same objective as DDPG. The potential issue is that 1) we get some numerical issues exponentiating a large number, and 2) the percent of actions with non-vanishing gradients becomes lower.

One way to think about it is that AWR acts like a filter. If the action has enough advantage, increase its probability. Otherwise do nothing. DDPG acts like an optimization problem. For every state, find the action that is the best, and memorize this mapping. AWR has the benefit that it only trains on state-action pairs in the data, which is good for offline RL, but it is also less efficient.

Increasing the temperature helps, but not as much as DDPG. We still have high standard deviation.

Conclusion: In maze2d, don't use AWR for policy extraction with a Gaussian head. Use discretization, or use DDPG.

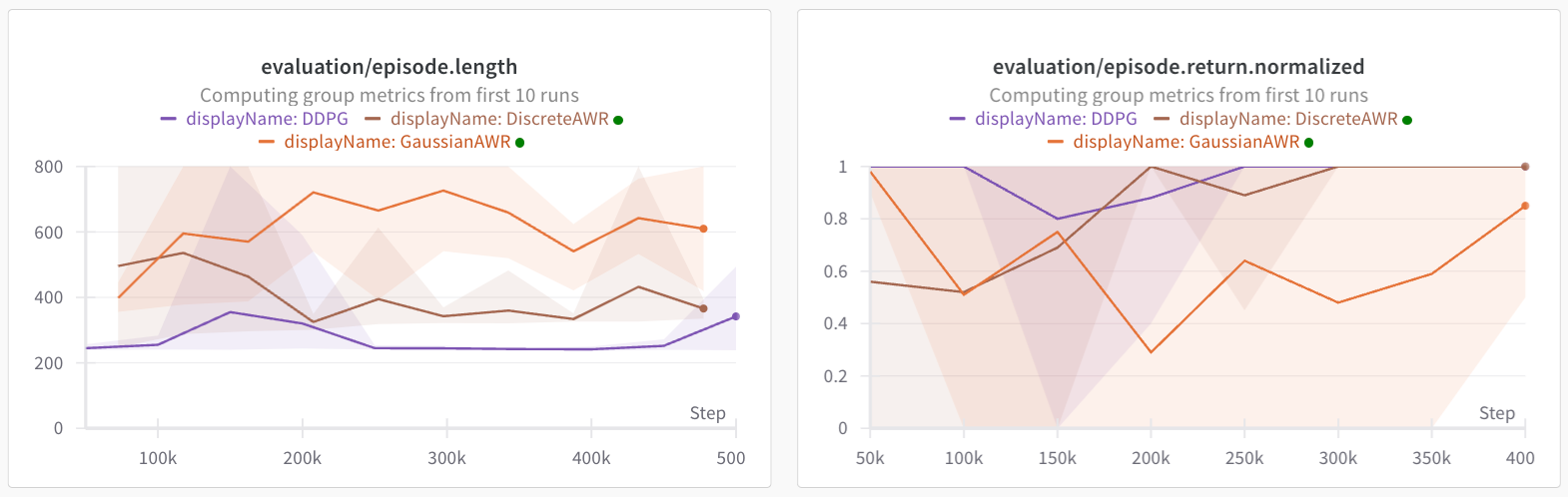
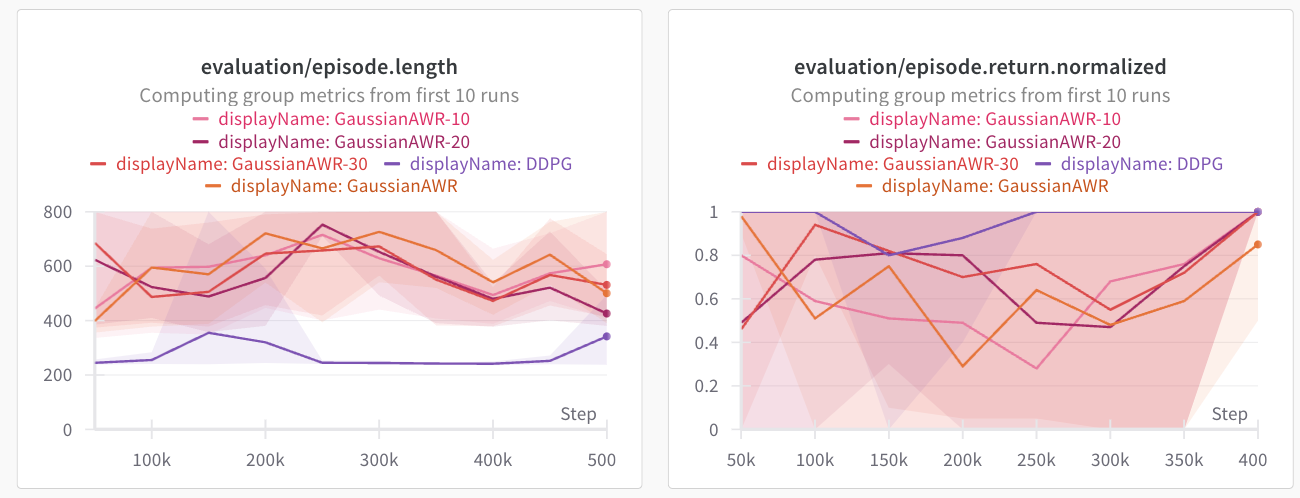
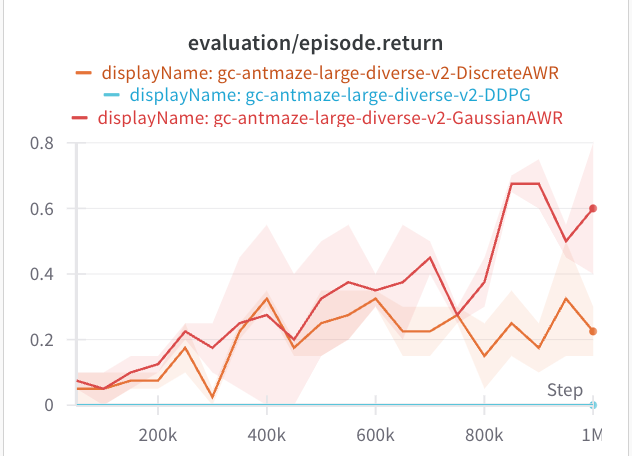
DDPG does the best on maze2d. Highest success rate, and also shortest time until completion.

How about other environments? I tried the same tactics on other envs, and here's what we get. For the full AntMaze, and on D4RL half-cheetah, the AWR style extraction actually performs the best.

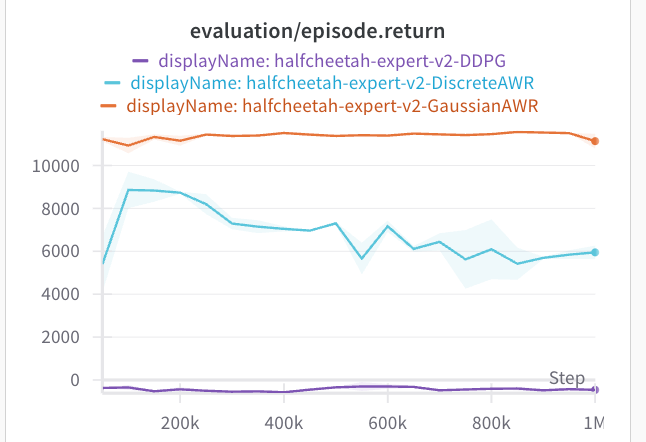
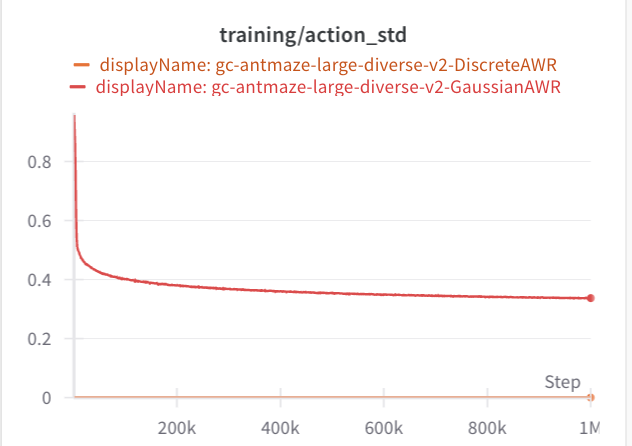
In both of these cases, the standard deviation via AWR is much lower. Both of these offline datasets are collected from expert data. So the data is naturally unimodal, which may be why AWR does not have an issue. If we look at the standard deviations, they are much lower than the maze2d experiments. All of these envs use an action space of (-1, 1).

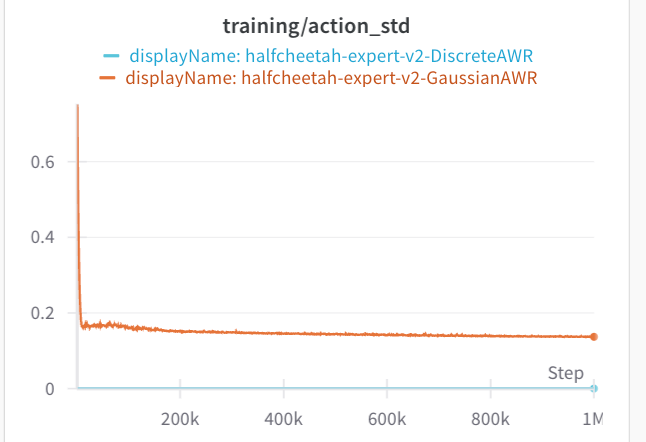
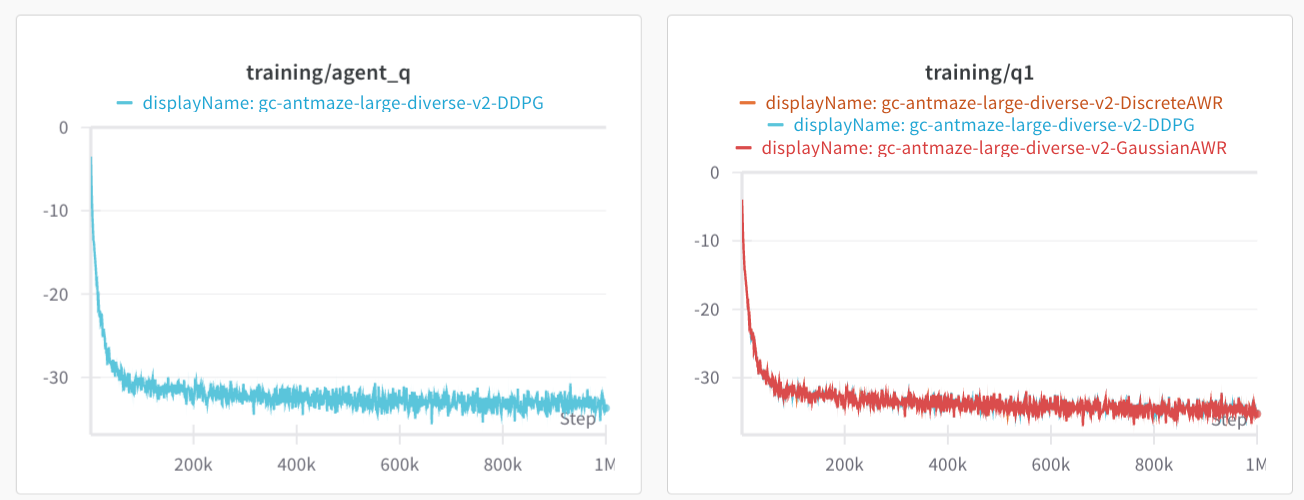
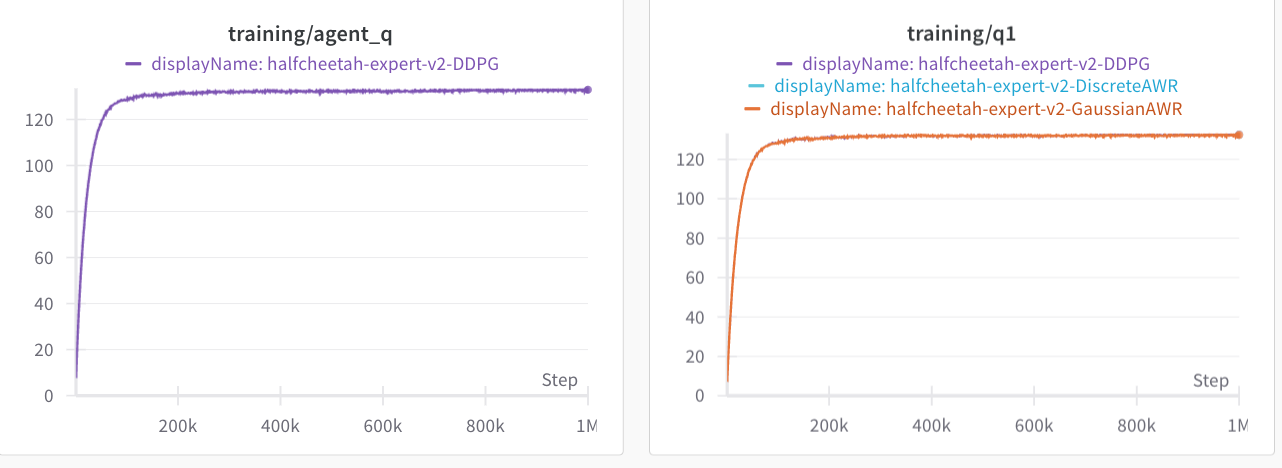
Why does DDPG do so bad? I am not sure. If we look at the average IQL Q-values, along with the average Q-values that during the policy optimization step, they look equal for both envs. Then again, what we really should look at are the advantages, which might be small in comparison to the value at each state. Likely, DDPG extraction is exploiting some errors in the Q-value network. Both AntMaze and half-cheetah do not provide dense coverage of the action space.


If we look at ExoRL cheetah-run, which does have dense coverage of the action space, we get a different story.

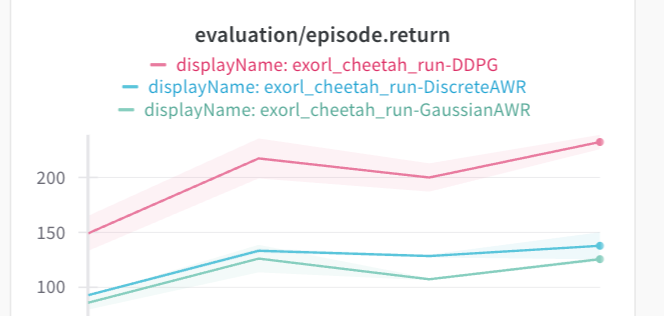
DDPG is better again. So, it seems like there are two categories here.

  • If the dataset has dense coverage, DDPG will solve the multimodality issues of AWR and perform better.
  • But without dense coverage, DDPG will overfit to the Q-function errors and learn a degenerate policy.

Results: On maze2d and ExoRL, DDPG performs decently better. On AntMaze and D4RL, AWR works and DDPG gets zero reward.

There's some clear room for improvement here – if the DDPG is prevented from overfitting on the sparse-data environments, likely it can outperform the AWR policy performance.