StampCA: Growing Emoji with Conditional Neural Cellular Automata

When a baby is born, it doesn’t just appear out of nowhere -- it starts as a single cell. This seed cell contains all the information needed to replicate and grow into a full adult. In biology, we call this process morphogenesis: the development of a seed into a structured design.

Of course, if there’s a cool biological phenomenon, someone has tried to replicate it in artificial-life land. One family of work examines Neural Cellular Automata (NCA), where a bunch of cells interact with their neighbors to produce cool emergent designs. By adjusting the behavior of the cells, we can influence them to grow whatever we want. NCAs have been trained to produce a whole bunch of things, such as self-repairing images, patternscapes, soft robots, and Minecraft designs.

A common thread in these works is that a single NCA represents a single design. Instead, I wanted to explore conditional NCAs, which represent design-producing functions rather than single designs. The analogy here is DNA translation -- our biologies don’t just define our bodies, they define a system which translates DNA into bodies. Change the DNA, and the body changes accordingly.

This post introduces StampCA, a conditional NCA which acts like a translation network. In StampCA, the starting cell receives an encoding vector, which dictates what design it must grow into. StampCA worlds can mimic the generative capabilities of traditional image networks, such as an MNIST-digit GAN and an Emoji-producing autoencoder. Since design-specific information is stored in cell state, StampCA worlds can 1) support morphogenetic growth for many designs, and 2) grow them all in the same world.

At the end, I’ll go over some thoughts on how NCAs relate to work in convnets, their potential in evo-devo and artificial life, and why I’m pretty excited about them looking ahead.

Neural Cellular Automata: How do they work?

First, let’s go over how an NCA works in general. The ideas here are taken from this excellent Distill article by Mordvintsev et. al. Go check it out for an nice in-depth explanation.

The basic idea of an NCA is to simulate a world of cells which locally adjust based on their neighbors. In an NCA, the world is a grid of cells. Let’s say 32 by 32. Each cell has a state, which is a 64-length vector. The first four components correspond to RGBA, while the others are only used internally.

Every timestep, all cells will adjust their states locally. Crucially, cells can only see the states of themselves and their direct neighbors. This information is given to a neural network, which then updates the cell's state accordingly. The NCA will iterate for 32 timesteps.

The key idea here is to learn a set of local rules which combine to form a global structure. Cells can only see their neighbors, so they need to rely on their local surroundings to figure out what to do. Again, the analogy is in biological development -- individual cells adjust their structure based on their neighbors, creating a functional animal when viewed as a whole.

In practice, we can define an NCA as a 3x3 convolution layer, applied recursively many times. This convolutional kernel represents a cell's receptive field – each cell updates its own state based on the states of its neighbors. This is repeated many times, until a final result is produced. Since everything is differentiable, we can plug in our favorite loss function and optimize.

By being creative with our objectives, we can train NCAs with various behaviors. The classic objective is to start with every cell set to zero except a single starting cell, and to grow a desired design in N timesteps. We can also train NCAs that maintain designs by using old states as a starting point, or NCAs which repair designs by starting with damaged states. There’s a lot of room for play here.

The common shortcoming here is that the NCA needs to be retrained if we want to produce a different design. We’ve successfully learned an algorithm which locally generates a global design -- now can we learn an algorithm which locally generates many global designs?

StampCA: Conditional Neural Cellular Automata

One way to view biological development is as a system of two factors: DNA and DNA translation. DNA produces a code; a translation system then creates proteins accordingly. In general, the same translation system is present in every living thing. This lets evolution ignore the generic heavy work (how to assemble proteins) and focus on the variation that matters for their species (which proteins to create).

The goal of a conditional NCA is in the same direction: separate a system which grows designs from a system which encodes designs. The key distinction is that encodings are design-specific, whereas the growth system is shared for all designs.

It turns out that the NCA formulation gives us a straightforward way to do this, which we’ll refer to as StampCA. In a typical NCA, we initialize the grid with all zeros except for a seed cell. Instead of initializing this seed cell with a constant, let’s set its state to an encoding vector. Thus, the final state of the NCA becomes a function of its neural network parameters along with the given encoding.

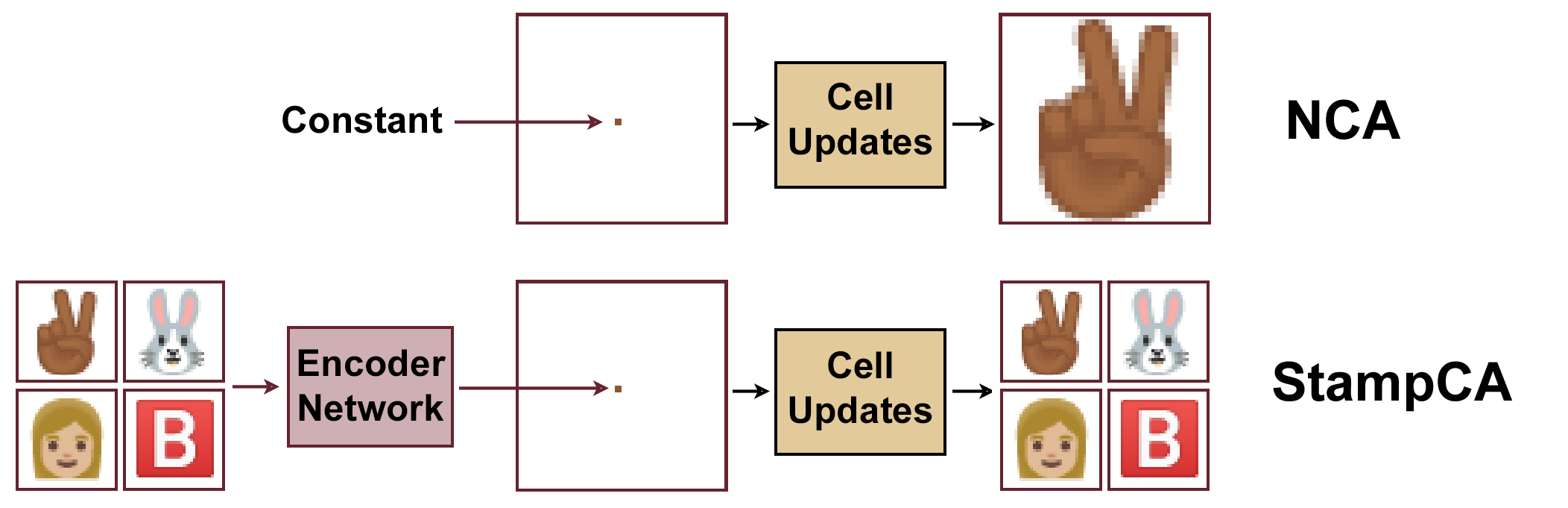
Armed with this, we can construct an autoencoder-type objective. Given a desired design, an encoder network first compresses it into an encoding vector. This encoding vector is used as the initial state in the NCA, which then iterates until a final design has been created. We then optimize everything so the final design matches the desired design.

A correctly-trained StampCA learns general morphogenesis rules which can grow an arbitrary distribution of designs. There are two main advantages over single-design NCAs:

1. StampCAs can grow new designs without additional training
2. Many designs can all grow in the same world

Let’s look at some examples on Emoji and MNIST datasets.

StampCA Autoencoder: Growing Emojis

The original Distill paper trained NCAs to grow emojis, so let’s follow suit. We’ll take a dataset of ~3000 32x32 emojis from this font repo. Our aim here is to train a StampCA which can grow any emoji in the dataset.

After training for about 4 hours on a Colab GPU, here’s the outputs:

Overall, it’s doing the right thing! A single network can grow many kinds of emoji.

For a StampCA network to correctly work, two main problems need to be solved: cells need to share the encoding information with each other, and cells need to figure out where they are relative to the center.

A cool thing about StampCAs is that multiple designs can grow in the same world. This works because all designs share the same network, they just have different starting seeds. Since NCAs by definition only affect their local neighbors, two seeds won’t interfere with each other, as long as they’re placed far enough apart.

StampCA GAN: Learning fake MNIST

A nice part about conditional NCAs is that they can approximate any kind of vector-to-image function. In the Emoji experiment we used an autoencoder-style loss to train NCAs that could reconstruct images. This time, let's take a look at a GAN objective: given a random vector, grow a typical MNIST digit.

OK, in an ideal world, this setup would be pretty straightforward. A GAN setup involves a generator network and a discriminator network. The generator attempts to produce fake designs, while the discriminator attempts to distinguish between real and fake. We train these networks in tandem, and over time the generator learns to produce realistic-looking fakes.

It turns out that this was a bit tricky to train, so I ended up using a hack. GANs are notoriously hard to stabilize, since the generator and discriminator need to be around the same strength. Early on, NCA behavior is quite unstable, so the NCA-based generator has a hard time getting anywhere.

Instead, the trick was to first train a traditional generator with a feedforward neural network. This generator learns to take in a random vector, and output a realistic MNIST digit. Then, we train an NCA to mimic the behavior of the generator. This is a more stable objective for the NCA to solve, and it eventually learns to basically match the generator's performance.

Discussion

First off, you can replicate these experiments through these Colab notebooks, here for the Emojis and here for the MNIST.

The point of this post was to introduce conditional NCAs and show that they exist as a tool. I didn't focus much on optimizing for performance, so I didn't spend much time tuning hyperparameters or network structures. If you play around with the models, I'm sure you can improve on the results here.

An NCA is really just a fancy convolutional network, where the same kernel is applied over and over. If we view things this way, then it's easy to plug in an NCA to whatever kind of image-based tasks you're interested in.

The interesting part about NCAs are that it becomes easy to define objectives that last over time. In this work, we cared about NCAs that matched the appearance of an image after a certain number of timesteps. We could have also done more complicated objectives: e.g, grow into a pig emoji after 50 timesteps, then transform into a cow emoji after 100.

The other aspect distinguishing NCAs are their locality constraints. In an NCA, it's guaranteed that a cell can only interact with its direct neighbors. We took advantage of this by placing multiple seeds in the same world, since we can be confident they won't interfere with one another. Locality also means we can increase the size of an NCA world to an arbitrary size, and it won't change the behavior at any location.

Looking ahead, there are a bunch of weirder experiments we can do with linking NCAs to task-based objectives. We could view an NCA as defining a multi-cellular creature, and train it to grow and capture various food spots. We can also view NCAs as communication systems, since cells have to form channels to tranfer information from one point to another. Finally, there's a bunch of potential in viewing NCAs as evo-devo systems: imagine an NCA defining a plant which dynamically adjusts how it grows based on the surroundings it encounters.

Code for these experiments is availiable at these notebooks. Feel free to shout at me on Twitter with any thoughts.

@article{frans2021stampca,
  title   = "StampCA: Growing Emoji with Conditional Neural Cellular Automata",
  author  = "Frans, Kevin",
  journal = "kvfrans.com",
  year    = "2021",
  url     = "http://kvfrans.com/stampca-conditional-neural-cellular-automata/"
}